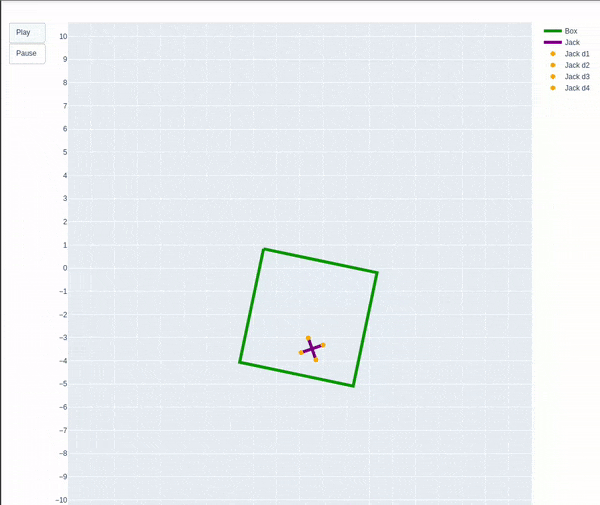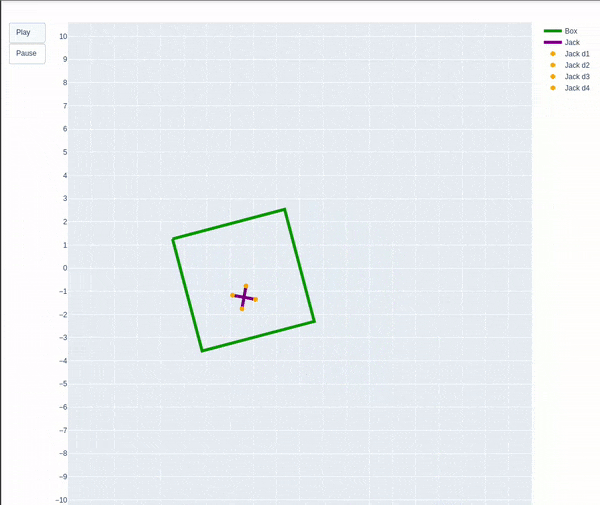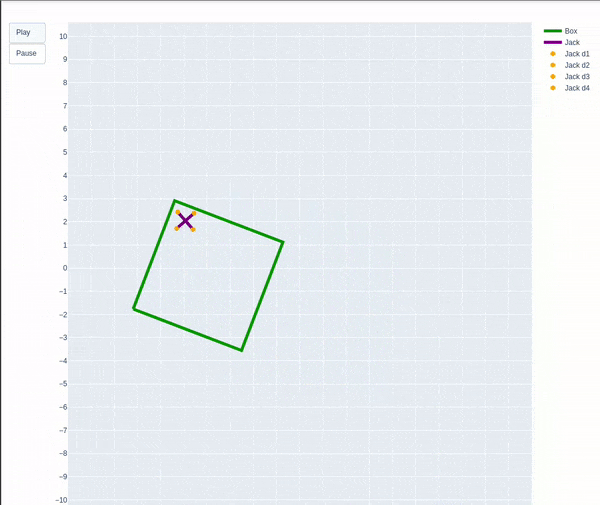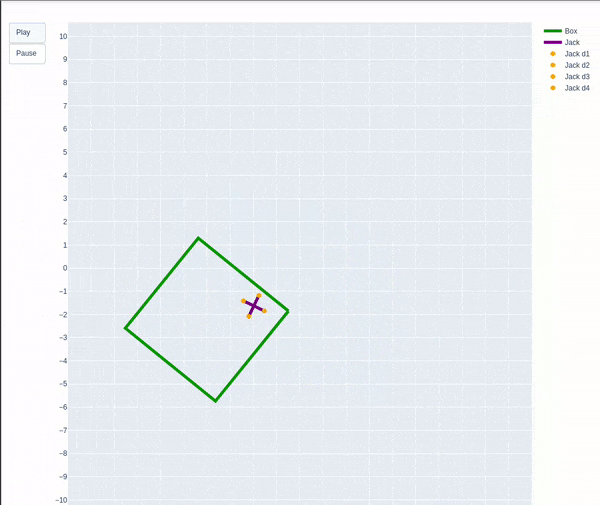
Overview

To simulate and animate a dynamic system of a jack in a box when the box is shaken. We are considering a side view in 2-D.

The configuration variables are:
q = [x_box, y_box, θ_box, x_jack, y_jack, θ_jack]
Below image depicts the frames I used.

Description

Rigid Body transformations
The transforms from the center of body to the world for both the box and the jack are found.
Next, the transforms of b1,b2,b3 and b4 of the box to b of the box; the transforms from d1, d2,d3,d4 of the jack to d of the jack.
To find the d1,d2,d3,d4 transforms of the jack with respect to the b1 of the box;
d1,d2,d3,d4 transforms of the jack with respect to the b2 of the box;
d1,d2,d3,d4 transforms of the jack with respect to the b3 of the box
d1,d2,d3,d4 transforms of the jack with respect to the b4 of the box
we calculate the inverse of the g_bb1, g_bb2, g_bb3 and g_bb4


Forces and Constraints

An external force of 700*sin(pi*t) is applied on the box in the x direction. A sinusoidal type of force provides a back and forth shaking motion. 700 is the amplitude and pi*t is the period; frequency=2pi/period.
And another external force of magnitude of the gravitational force acting on the box (Total mass of box*gravity*height of the box from its center of mass with respect to the world frame) is applied in the opposite direction of that gravitational force to prevent the Box from falling down and going outside the scene.

The constraint for jack's impact with the sides of box corresponding to the b1 and b3 frame is the x-axis.
The constraint for jack's impact with the sides of box corresponding to the b2 and b4 frame is the y-axis.


Impact Update Laws
Forces of gravity are acting on the total mass of the box and on the total mass of the jack.
Calculate the kinetic energy and potential energy acting on each
Langrangian = Total Kinetic energy (i.e. Box + Jack) – Total Potential energy ( i.e. Box + Jack)
For calculating the inertia Izz to use in the KE, I took 4 point masses at the corners for each, the box and the jack.
From the Langrangian we can get the Euler-Langrangian Equation and then a Euler-Langrange matrix equation where we have one side as the previous Euler Langrangian terms and the other side as the Force matrix in the q configuration.
Then find the impact equations by using the constraints matrix, substituting values in the tau plus (after impact)
Checking for impact conditions and only when there is impact solving for them.


Graphs

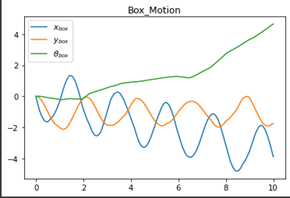
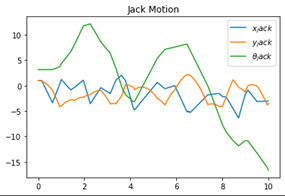
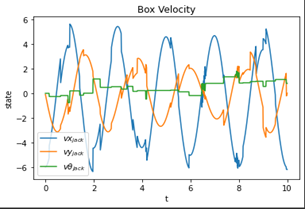
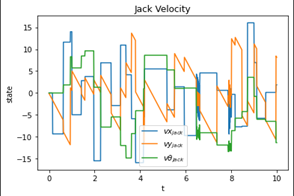
Observation
The box is shaking as expected which slowly starts to die down until the impact from the jack adds a torque to the box. The box’s height is maintained to an extent and not changing much with respect to its center of mass to the world frame and it does not fall out of the scene.
The jack due to the force of gravity acting on it always tries to fall down while staying inside the box.
The impact of the jack on the walls of the box causes the jack itself to rotate as well as bounce from one wall to another.